TORIC IOL POWER CALCULATION

Introduction

Toric intraocular lenses (TIOL) have gained increasing popularity in the last years. They are considered first choice for moderate and high astigmatism and are implanted by 61% of all surgeons in the ESCRS (European Society of Cataract & Refractive Surgeons). Of all intraocular lenses (IOL), toric IOLs draw maximum interest among ophthalmic surgeons [1]. Obviously, toric lenses have to remain in stable positions after implantation bearing in mind that for every 10 degrees of misalignment, there is one third loss of toric correction. While some time ago this was still a problem, toric IOLs of today are significantly less affected by lens rotation. Another disturbing issue with toric lenses has also been fixed in the meantime: according to a new ISO standard [2], it is necessary for the dioptric properties of a toric IOL to be labelled as spherical equivalent (SEQ) and cylinder power (CYL) and not as spherical (SPH) and cylindrical (CYL) power. The coexistence of both labelling methods has created considerable confusion in the past.

Toric IOL calculation General

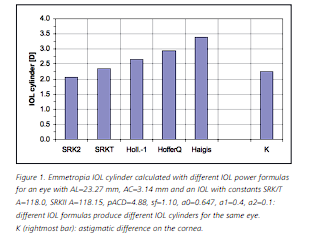
Different methods are in use to calculate the powers of a toric lens: for each meridian (flat as well as steep) a separate IOL calculation may be carried out with one of the classical IOL formulas. As a result of this 2-meridian approach, two powers – F and S – are obtained. The difference S-F, then, gives the cylinder, the sum (F+S) / 2 the spherical equivalent SEQ of the lens to be implanted. Another option is to start out from the SEQ for the IOL and the astigmatic difference in the cornea. The latter is then translated by a constant factor (e.g.1.4) from the corneal to the IOL plane resulting in the CYL value of the IOL. In the internet, many toric IOL calculators of this kind can be found on the pages of IOL manufacturers who thus offer a simple way for toric IOL calculation. Implementations using a constant translation factor instead of the ‘real’ IOL position.

in the eye, however, are suffering from systematic errors as they are valid only for an average eye. Furthermore, these calculators ask for a SEQ value without specifying which formula to use for its derivation; different IOL formulas, however, will produce different lens powers. Likewise, if the IOL cylinder is calculated with the 2-meridian method, the formula selection again plays an important role as different IOL formulas also produce different astigmatic differences (cf Fig.1). Additional inaccuracies are created by some IOL formulas (HofferQ, Holladay-1 and SRK/T), which use the corneal power as a predictor for the effective lens position (ELP): different K-values in different meridians are equivalent  to different ELPs for the toric IOL.

Haigis-T formalism

With the Haigis-T formula for toric IOL calculation which is included in the new ZEISS IOLMaster 700 it is possible to overcome the problems described above. Based on the standard Haigis formula, the well-proven IOL constants published in the ULIB table [3] can be used. Also, by extending the Haigis-L approach [4] to two meridians, astigmatic post-refractive-surgery eyes can be made allowance for.

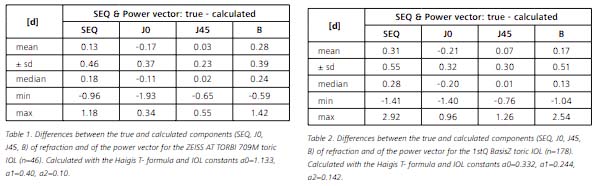
Clinical results

The Haigis-T formalism was retrospectively applied to 2 toric IOLs for which preoperative biometry and keratometry data obtained with the IOLMaster and stable postoperative refractive results were available. A total of n=178 patient data sets for the 1stQ BasicZ toric IOL and n=46 for the ZEISS AT TORBI 709M was evaluated to assess the performance of this new formalism. As IOL constants for the 1stQ BasisZ toric IOL (a0=0.332, a1=0.244, a2=0.142), the respective values of the 1stQ BasisZ rotational symmetric IOL from the ULIB table of Feb. 09, 2012 were taken. The constants for the ZEISS AT TORBI 709M (a0=1.133, a1=0.40, a2=0.10) were derived from a separate data set of n=49 patients implanted with the same lens type. Tabs.1-2 and Figs.2-5 show the results for the 2 IOLs in terms of the differences between the true and calculated components of refraction and the power vector [5]. The power vector characterized by its magnitude B allows an easy comparison of directional data like refractive changes: its length is a direct measure for its blur strength. The tables and figures show for both lenses examined good agreement between the calculated and actually achieved values for the SEQ as well as the power vector. For the 1stQ lens, the differences between predicted and measured SEQ are 0.31 ± 0.55 D, for the power vector B 0.17 ± 0.51 D. The respective data for the ZEISS lens are 0.13 ± 0.46 D (SEQ) and 0.28 ± 0.39 (power vector).